Welcome to Maths.ai, your reliable AI-based companion for solving challenging math problems! In this article, we’ll dive into the world of logarithms, exploring their properties and presenting a comprehensive step-by-step guide to solve log equations. With the assistance of our Maths.ai, we’ll walk you through the process and provide real-life examples to solidify your understanding.
Section 1: Understanding Logarithms
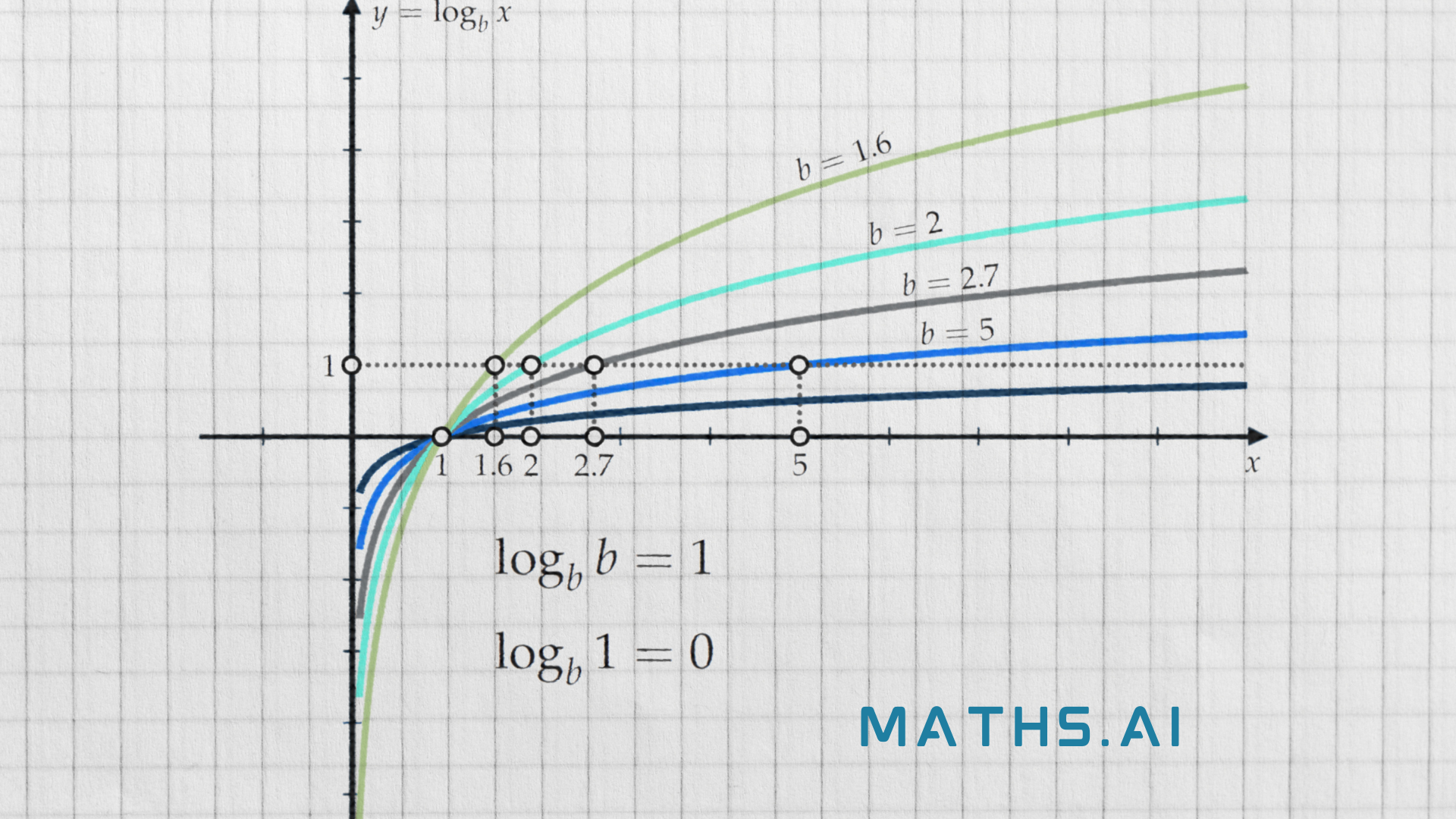
Before we jump into solving logarithmic equations, it’s crucial to grasp the concept of logarithms. A logarithm is the inverse operation of exponentiation. In other words, it answers the question, “What exponent do I need to raise a particular base to, to obtain a given value?” The notation for a logarithm is as follows:
If \(b^x = y\), then \(\log_{b}(y) = x\).
Here, \(b\) is the base, \(x\) is the exponent, and \(y\) is the result of the exponentiation. Logarithms are particularly useful in solving problems involving exponential growth, decay, and complex calculations.
Section 2: Properties of Logarithms
Before we proceed with solving logarithmic equations, let’s review some key properties of logarithms:
1. Product Rule: \(\log_b(xy) = \log_b(x) + \log_b(y)\)
2. Quotient Rule: \(\log_b\left(\frac{x}{y}\right) = \log_b(x) – \log_b(y)\)
3. Power Rule: \(\log_b(x^n) = n \cdot \log_b(x)\)
These properties allow us to manipulate logarithmic expressions and simplify complex equations into more manageable forms.
Section 3: Solving Basic Logarithmic Equations
Now, let’s delve into solving basic logarithmic equations. Consider the equation:
\(\log_2(x) = 3\)
Step 1: Recognize the Base and Result
Identify the base of the logarithm, which is \(2\) in this case, and the result of the logarithmic expression, which is \(3\).
Step 2: Rewrite the Equation in Exponential Form
To solve for \(x\), rewrite the equation in exponential form:
\(2^3 = x\)
Step 3: Evaluate the Exponent
Compute the result of \(2^3\):
\(2^3 = 8\)
Step 4: Determine the Solution
The value of \(x\) that satisfies the equation \(\log_2(x) = 3\) is \(8\).
Section 4: Solving Logarithmic Equations with Variables
Now, let’s tackle a more complex logarithmic equation involving variables:
\(\log_3(x+2) – \log_3(x) = 2\)
Step 1: Combine Logarithms
Apply the quotient rule to combine the two logarithms:
\(\log_3\left(\frac{x+2}{x}\right) = 2\)
Step 2: Express Equation in Exponential Form
Rewrite the equation in exponential form:
\(3^2 = \frac{x+2}{x}\)
Step 3: Solve for \(x\)
To solve for \(x\), isolate \(x\) on one side of the equation:
\(9x = x + 2\)
Step 4: Simplify and Solve
Combine like terms and isolate \(x\) on one side:
\(9x – x = 2\)
\(8x = 2\)
\(x = \frac{2}{8} = \frac{1}{4}\)
Step 5: Verify Solution
Check if the solution \(x = \frac{1}{4}\) is valid by ensuring that \(x\) is positive in the original equation:
\(\log_3\left(\frac{\frac{1}{4}+2}{\frac{1}{4}}\right) – \log_3\left(\frac{1}{4}\right) = \log_3\left(\frac{\frac{9}{4}}{\frac{1}{4}}\right) – \log_3\left(\frac{1}{4}\right) = \log_3(9) – \log_3(1) = 2 – 0 = 2\)
The solution \(x = \frac{1}{4}\) satisfies the original equation.
Section 5: Solving Logarithmic Equations with Advanced Techniques
In more advanced problems, logarithmic equations may require additional techniques for simplification. Let’s consider an example:
\(\log_2(x^2 – 9) – \log_2(x+3) = 1\)
Step 1: Combine Logarithms
Apply the quotient rule to combine the two logarithms:
\(\log_2\left(\frac{x^2 – 9}{x+3}\right) = 1\)
Step 2: Express Equation in Exponential Form
Rewrite the equation in exponential form:
\(2^1 = \frac{x^2 – 9}{x+3}\)
Step 3: Solve for \(x\)
To solve for \(x\), isolate the expression on one side of the equation:
\(2(x+3) = x^2 – 9\)
Step 4: Expand and Simplify
Expand the left side of the equation:
\(2x + 6 = x^2 – 9\)
Step 5: Move All Terms to One Side
Move all terms to one side of the equation to obtain a quadratic equation:
\(x^2 – 2x – 15 = 0\)
Step 6: Factor and Solve
Factor the quadratic equation:
\((x-5)(x+3) = 0\)
Set each factor to zero and solve for \(x\):
\(x-5 = 0 \Rightarrow x = 5\)
\(x+3 = 0 \Rightarrow x = -3\)
Step 7: Verify Solutions
Check if the solutions \(x = 5\) and \(x = -3\) are valid by ensuring that the expressions inside the logarithms are positive:
For \(x = 5\):
\(\log_2(5^2 – 9) – \log_2(5+3) = \log_2(16) – \log_2(8) = 4 – 3 = 1\)
For \(x = -3\):
\(\log_2((-3)^2 – 9) – \log_2((-3)+3) = \log_2(0) – \log_2(0)\)
Since the expression inside the first logarithm is non-positive, the solution \(x = -3\) is invalid.
Congratulations! You have now mastered the art of solving logarithmic equations, thanks to the step-by-step guidance of Maths.ai . Remember the fundamental properties of logarithms and apply them to simplify and solve log equations. With practice, you’ll become adept at handling logarithms and excel in your mathematical journey. Keep exploring the fascinating world of mathematics with the support of Maths.ai, your online maths tutor for all your maths-related support.


One Comment