Setting the Stage
Welcome, fellow explorers, to the enthralling universe of Set Theory. In this first phase, we’ll lay the foundation for our expedition by understanding what sets are and how they shape the mathematical landscape.
Set: A magical container that holds distinct elements. Picture it as a box filled with objects, where each object is unique and contributes to the set’s identity.
Unveiling the Basics
Now that we have our set in place, it’s time to delve into the fundamental elements of set theory. In this phase, we’ll unravel the terminology and symbols that bring sets to life.
- Elements and Roster Notation: Learn how to list the members of a set using roster notation. For example, {1, 2, 3} represents a set with elements 1, 2, and 3.
- Set-builder Notation: Explore the concise way of defining sets with set-builder notation. {x | x is an even number} denotes a set of even numbers.
The Magic of Operations
As our understanding of sets grows, it’s time to unlock the magic of set operations. Just like wizards combining spells, we’ll combine sets to create new and exciting mathematical entities.
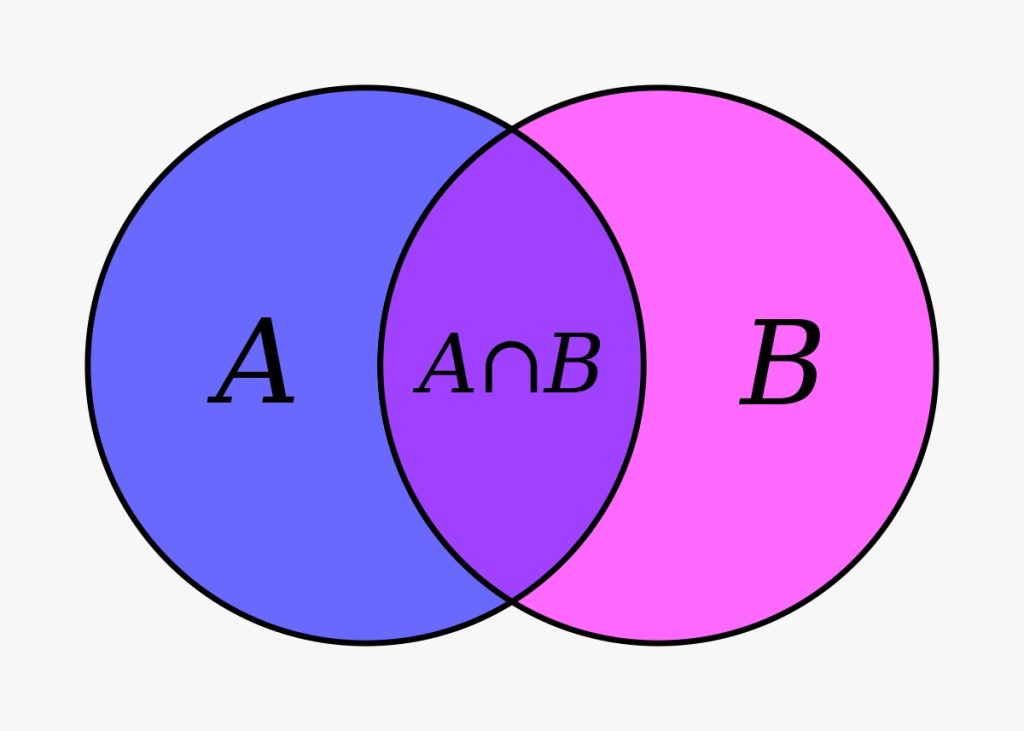
- Union (∪): Discover how to unite sets, merging their unique elements into a harmonious whole. The union of sets A and B is denoted as A ∪ B.
- Intersection (∩): Witness the beauty of commonality assets A and B intersect, revealing shared elements. The intersection of A and B is written as A ∩ B.
- Complement (‘): Explore the realm of opposites by finding the complement of a set. If A is our set, A’ is everything not in A.
Navigating Set Relationships
In this phase, we embark on a journey to understand how sets relate to each other. Just like constellations in the night sky, sets form patterns and connections that we’ll decode.
- Subset (⊆): Uncover the beauty of inclusion as one set becomes part of another. If every element in A is also in B, we say A is a subset of B (A ⊆ B).
- Superset (⊇): Witness the expansiveness of sets as one embraces the other. If every element in B is also in A, we declare B is a superset of A (B ⊇ A).
Applications and Real-world Connections
Our journey concludes with the practical applications of set theory. From Venn diagrams illustrating complex relationships to real-world scenarios, we’ll witness the omnipresence of sets in our mathematical odyssey.
- Venn Diagrams: Unravel the power of visualization as we employ Venn diagrams to represent intricate set relationships.
- Real-world Examples: Explore how set theory finds applications in diverse fields – from categorizing data in statistics to organizing information in databases.
Read about different types of diagrams here